Matriks adalah suatu kumpulan besaran (variabel dan konstanta) yang tersusun dalam baris dan kolom berbentuk persegi panjang. Matriks merupakan suatu cara visualisasi variabel yang merupakan kumpulan dari angka-angka atau variabel lain, misalnya vektor. Dengan representasi matriks, perhitungan dapat dilakukan dengan lebih terstruktur. Pemanfaatannya misalnya dalam menjelaskan persamaan linier, transformasi koordinat, dan lainnya. Matriks seperti halnya variabel biasa dapat dimanipulasi, seperti dikalikan, dijumlah, dikurangkan dan didekomposisikan.

Suatu matriks biasanya dinotasikan dengan huruf kapital ditebalkan (misal matriks A, dituliskan dengan A). Sebagai contoh matriks, perhatikan tabel yang memuat informasi biaya pengiriman barang dari 3 pabrik ke 4 kota berikut ini:
Pabrik | Kota | |||
Kota 1 | Kota 2 | Kota 3 | Kota 4 | |
Pabrik 1 | 5 | 2 | 1 | 4 |
Pabrik 2 | 2 | 3 | 6 | 5 |
Pabrik 3 | 7 | 6 | 3 | 2 |
Tabel di atas jika disajikan dalam bentuk matriks akan menjadi seperti berikut:
Kolom1 | Kolom2 | Kolom3 | Kolom4 | ||
5 | 2 | 1 | 4 | Baris1 | |
A = | 2 | 3 | 6 | 5 | Baris2 |
7 | 6 | 3 | 2 | Baris3 |
Matriks di atas, kita sebut saja matriks A, memiliki tiga baris yang mewakili informasi Pabrik (1, 2, dan 3) dan empat kolom yang mewakili informasi Kota (1, 2, 3, dan 4). Sedangkan informasi biaya pengiriman dari masing-masing pabrik ke tiap-tiap kota, diwakili oleh perpotongan baris dan kolom. Sebagai contoh, perpotongan baris 1 dan kolom 1 adalah 5, angka 5 ini menunjukkan informasi biaya pengiriman dari pabrik 1 ke kota 1, dst. Secara umum, bentuk matriks di atas dapat dituliskan seperti berikut:
a11 | a12 | a13 | a14 | |
A = | a21 | a22 | a23 | a24 |
a31 | a32 | a33 | a34 |
dimana, pada notasi elemen matriks, angka sebelah kiri adalah informasi baris sedangkan angka di kanan adalah informasi kolom, contoh a23 berarti nilai yang diberikan oleh baris ke-2 dan kolom ke-3.
Setiap bilangan pada matriks disebut elemen(unsur) matriks. Letak suatu unsur matriks ditentukanoleh baris dan kolom di mana unsur tersebut berada. Misalnya, pada matriks di atas unsur 25 trletak pada baris ke-3 dan pada kolom ke-2. Suatu matriks dinyatakan dengan huruf kapital A , B , C ,. . . . dan seterusnya, sedangkan unsur matriks dinyatakan dengan huruf kecil a, b , c , . . ., dan seterusnya.
Contoh :
Matriks A mempunyai dua baris dan dua kolom. Oleh karena itu kita katakan bahwa matriks A berordo 2 x 3 ditulis A2x3 atau ( a23 ) .Ordo suatu matriks ditentukan oleh banyaknya baris dan banyaknya kolom dalam matriks tersebut.


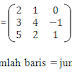

0 komentar:
Posting Komentar
Boss-boss yang baik tolong dikomteri ya Tulisan aku ini
hehehehehe.....