1. Penjumlahan dan pengurangan Matriks
Syarat : ukuran matrik harus sama.
Jika A = (aij) dan B = (bij), matrik berukuran sama,
Jika A = (aij) dan B = (bij), matrik berukuran sama,
maka A + B/ A - B adalah suatu matrik C = (cij)
dimana cij = aij + bij / aij - bij untuk setiap i dan jContoh :
Beberapa sifat yang berlaku pada penjumlahan matriks
1) A + B = B = A ( Sifat Komutatif )
2) (A + B) + C = A + ( B + C) ( Sifat Asosiatif )
3) A + 0 = 0 + A = A ( Sifat Identitas tambah )
2. Perkalian Bilangan Real dengan Matriks
Jika A suatu ordo m x n dan k suatu bilangan real (disebut juga sutu skalar), maka kA adalah metriks ordo m x n yang unsur-unsurnya diperoleh dengan memperkalikan setiap unsur matriks A dengan k. Perkalian seperti ini disebut perkalian skalar.
Jadi
Contoh :
Sifat-sifat perkalian matriks dengan bilangan real.
Jika a dan b bilangan real, maka :
1) ( a + b )A = aA + bA
2) a ( A + B ) = aA + aB
3) a( bA ) = (ab)A




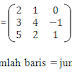

ada pertanyaan ni gan...
dapet soal dari dosen, matriks pembagian ada atau tidak???
terus tolong dijelasin ya, dosennya minta alasan...
mksh...