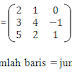Teori graf pertama kali dikembangkan oleh Leonhard Euler dalam memecahkan masalah jembatan Königsberg (tahun 1736). Permasalahannya adalah " Apakah bisa seseorang melalui sekali setiap jembatan yang menghubungkan kota-kota tersebut, dan kembali lagi ke kota dari mana ia berjalan".
Graf yang merepresentasikan jembatan Königsberg :
Simpul (vertex)--- menyatakan daratan
Ruas (edge) ---menyatakan jembatan
Bisakah melalui setiap jembatan tepat sekali dan kembali lagi ke tempat semula?
• Perjalanan Euler adalah :
Perjalanan dari suatu simpul kembali ke simpul tersebut dengan melalui setiap ruas tepat satu kali.
• Perjalanan Euler akan terjadi, jika :
- Graf terhubung.
- Banyaknya ruas yang datang pada setiap simpul adalah genap.
• Perjalanan Euler adalah :
Perjalanan dari suatu simpul kembali ke simpul tersebut dengan melalui setiap ruas tepat satu kali.
• Perjalanan Euler akan terjadi, jika :
- Graf terhubung.
- Banyaknya ruas yang datang pada setiap simpul adalah genap.
Definisi Graf
Graf G (V, E), adalah koleksi atau pasangan dua himpunan
(1) Himpunan V yang elemennya disebut simpul atau titik, atau vertex, atau point, atau node.
(2) Himpunan E yang merupakan pasangan tak terurut dari simpul, disebut ruas atau rusuk, atau sisi, atau edge, atau line.
Banyaknya simpul (anggota V) disebut order Graf G, sedangkan banyaknya ruas (anggota E) disebut ukuran (size) Graf G.
G1 adalah graf dengan
V = { 1, 2, 3, 4 }
E = { (1, 2), (1, 3), (2, 3), (2, 4), (3, 4) }
G2 adalah graf dengan
V = { 1, 2, 3, 4 }
E = { (1, 2), (2, 3), (1, 3), (1, 3), (2, 4), (3, 4), (3, 4) }
= { e1, e2, e3, e4, e5, e6, e7}
G3 adalah graf dengan
V = { 1, 2, 3, 4 }
E = { (1, 2), (2, 3), (1, 3), (1, 3), (2, 4), (3, 4), (3, 4), (3, 3) }
= { e1, e2, e3, e4, e5, e6, e7, e8}
(1) Himpunan V yang elemennya disebut simpul atau titik, atau vertex, atau point, atau node.
(2) Himpunan E yang merupakan pasangan tak terurut dari simpul, disebut ruas atau rusuk, atau sisi, atau edge, atau line.
Banyaknya simpul (anggota V) disebut order Graf G, sedangkan banyaknya ruas (anggota E) disebut ukuran (size) Graf G.
G1 adalah graf dengan
V = { 1, 2, 3, 4 }
E = { (1, 2), (1, 3), (2, 3), (2, 4), (3, 4) }
G2 adalah graf dengan
V = { 1, 2, 3, 4 }
E = { (1, 2), (2, 3), (1, 3), (1, 3), (2, 4), (3, 4), (3, 4) }
= { e1, e2, e3, e4, e5, e6, e7}
G3 adalah graf dengan
V = { 1, 2, 3, 4 }
E = { (1, 2), (2, 3), (1, 3), (1, 3), (2, 4), (3, 4), (3, 4), (3, 3) }
= { e1, e2, e3, e4, e5, e6, e7, e8}
- Pada G2, sisi e3 = (1, 3) dan sisi e4 = (1, 3) dinamakan ruas berganda atau ruas sejajar (multiple edges atau paralel edges), karena kedua sisi ini menghubungi dua buah simpul yang sama, yaitu simpul 1 dan simpul 3.
- Pada G3, sisi e8 = (3, 3) dinamakan gelung atau self-loop karena ia berawal dan berakhir pada simpul yang sama.